最大上升子序列和

题目：最大上升子序列和

一个数的序列 bi，当 b1<b2<…<bS 的时候，我们称这个序列是上升的。

对于给定的一个序列(a1,a2,…,aN)，我们可以得到一些上升的子序列(ai1,ai2,…,aiK)，这里1≤i1<i2<…<iK≤N。

比如，对于序列(1,7,3,5,9,4,8)，有它的一些上升子序列，如(1,7),(3,4,8)等等。

这些子序列中和最大为18，为子序列(1,3,5,9)的和。

你的任务，就是对于给定的序列，求出最大上升子序列和。

注意，最长的上升子序列的和不一定是最大的，比如序列(100,1,2,3)的最大上升子序列和为100，而最长上升子序列为(1,2,3)。

输入格式

输入的第一行是序列的长度N。

第二行给出序列中的N个整数，这些整数的取值范围都在0到10000(可能重复)。

输出格式

输出一个整数，表示最大上升子序列和。

数据范围

1≤N≤1000

输入样例：

7
1 7 3 5 9 4 8

输出样例：

18

题目分析:

​ 一看题目就知道是最长上升子序列模型，只不过这里求的是最大和，只需要对代码进行一部分修改即可。

​ DP分析过程如下：

​

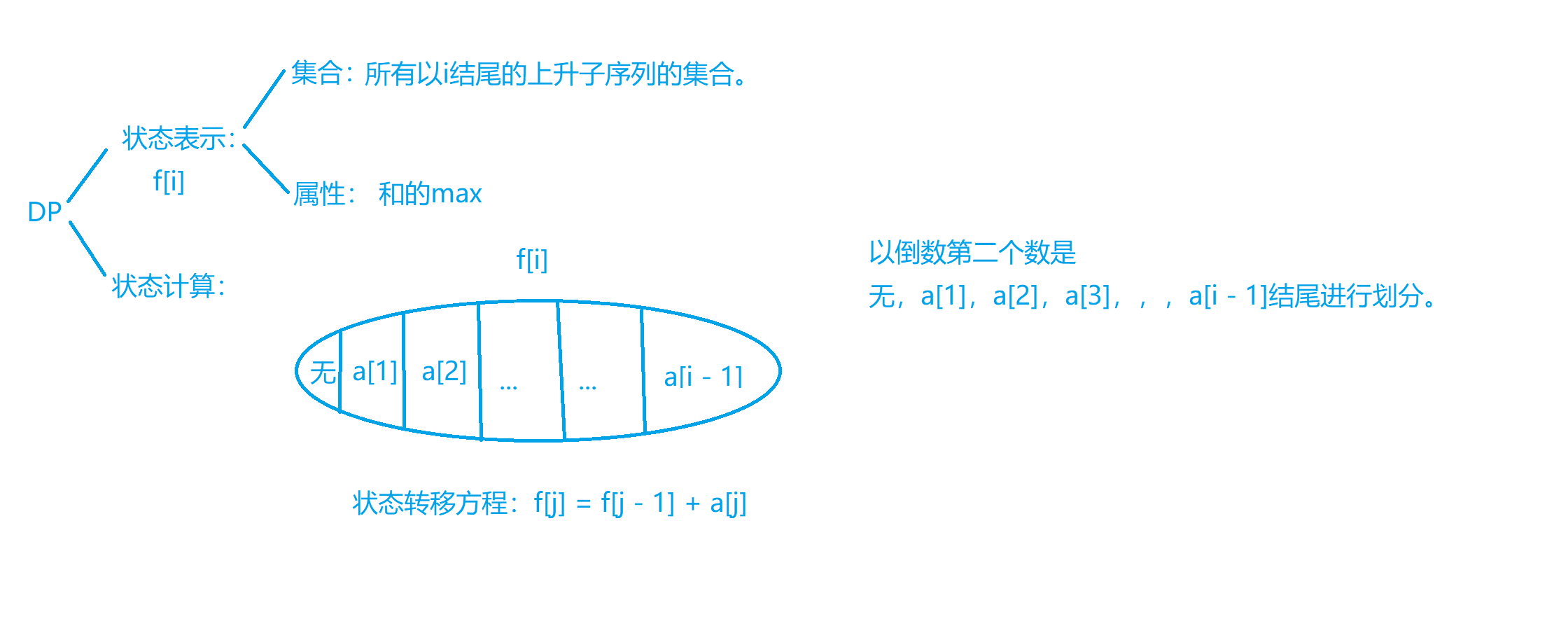
AC代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int n;
int f[N], a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    
    int res = 0;
    for (int i = 1; i <= n; i ++)
    {
        f[i] = a[i];	//求的是最大和，故需要加上当前数
        for (int j = 1; j < i; j ++)
            if (a[i] > a[j])
                f[i] = max(f[i], f[j] + a[i]);	//状态转移方程
        res = max(res, f[i]);
    }
    
    cout << res << endl;
    
    return 0;
}