线性DP

线性DP

1、数字三角形模型

数字三角形

描述：

​ 从某个顶点出发，走到最底层或者最底层的某个点，求该路径的数字和的最大值。

思路：

状态表示：f[i][j]
集合：所有从起点走到(i, j)的路径
属性：MAX

集合划分：以最后一个点是由左上方来的，还是右上方来的进行划分。

状态转移方程：f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + g[i][j];

代码模板：

for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= n + 1; j ++)
            f[i][j] = -2e9;

for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= i; j ++)
            f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + g[i][j];

注意：

​ 在这里DP问题时，初始化需要特别注意。

​ 这里的初始化有两种，目的都是为了处理负数的情况：

​ （1）第一种是按照模板那样写

​ （2）第二种是，直接用memset函数，将f数组全部设置为-INF，memset(f, -0x3f, sizeof g);

​ 此时需要将特判第一个点，将起点赋值为f[1][1] = g[1][1]，并在循环里从第二行开始处理，即跳过已经处理过的起点

拓展1：

​ 若地图是一个矩形，且求的是最小值，题目见

[最低通行费]: https://www.acwing.com/problem/content/1020/ “ “

思路：

​ 初始化时由于我们发现第一排只能是从左到右更新，第一列只能是从上到下更新，故需要特判，具体见下述代码。但我们发现这样会导致起点无法遍历，故需要直接单独处理起点。

代码：

memset(f, 0x3f, sizeof f);
    f[1][1] = g[1][1];
    
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= n; j ++)
            {
                if (i > 1) f[i][j] = min(f[i - 1][j] + g[i][j], f[i][j]);
                if (j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + g[i][j]);
            }

拓展2：

​ 若整个地图走了两遍，该如何处理？例题，见

[方格取数]: https://www.acwing.com/problem/content/1029/ “ “

​ 题目类似的还有

[传纸条]: https://www.acwing.com/problem/content/277/ “传纸条”

思路：

​ 只走一次：

​ f[i][j]表示所有从(1,1)走到(i,j)的路径的最大值

​ f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j]；

​ 走两次：

​ f[i1,j1,i2,j2]表示所有从(1,1),(1,1)分别走到(i1,j1),(i2,j2)路径的最大值。

​ 如何处理“同一个格子不能被重复选择”？
​ 分析后发现，只有当i1 + j1 == i2 + j2时，两条路径的格子才可能重合，
​ 于是可以根据这条性质将思维优化成三维，

​ 集合：f[k,i1,i2]表示所有从(1,1),(1,1)走到(i1,k-i1),(i2,k-i2)的路径的最大值
​ k表示两条路线当前走到的格子的横纵坐标之和

​ 属性：max

​ 状态计算：
​ 以最后一步是从往下走还是往右走进行划分，因为有两次走法，所以被分成了四种情况
​ 下下、下右、右下、右右

代码模板：

for (int k = 2; k <= n + n; k ++)   //枚举横纵坐标之和
        for (int i1 = 1; i1 <= n; i1 ++)    //枚举第一次走的横坐标
            for (int i2 = 1; i2 <= n; i2 ++)    //枚举第二次走的横坐标
            {
                int j1 = k - i1, j2 = k - i2;   //计算出两次走的纵坐标
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = g[i1][j1];  //如果两个坐标相等，只加一次，因为第二次走这里，已经被拿走清空了
                    if (i1 != i2) t += g[i2][j2];   //坐标不相同，就两个位置全加上
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);   //下 下
                    x = max(x, f[k - 1][i1 - 1][i2] + t);       //下 右
                    x = max(x, f[k - 1][i1][i2 - 1] + t);       //右 下
                    x = max(x, f[k - 1][i1][i2] + t);            //右 右
                }
            }

注意：

（1）为什么下面四个状态转移方程能代表四种状态？

​ 原因是，因为k 变小了1，先不看最后一步，如果i变小1，则j就不用变；如果i没有变，则j就需要变小1；

​ 上述两种情况刚好对应了最后一步是向下、右走，的横纵坐标变化情况，又因为是两次一起走，故有四种情况。

​ x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); //下 下
​ x = max(x, f[k - 1][i1 - 1][i2] + t); //下 右
​ x = max(x, f[k - 1][i1][i2 - 1] + t); //右 下
​ x = max(x, f[k - 1][i1][i2] + t); //右 右

​ （2）在开数组的时候，第一维即横纵坐标之和一定要开数据范围的两倍

2、最短编辑距离

描述：

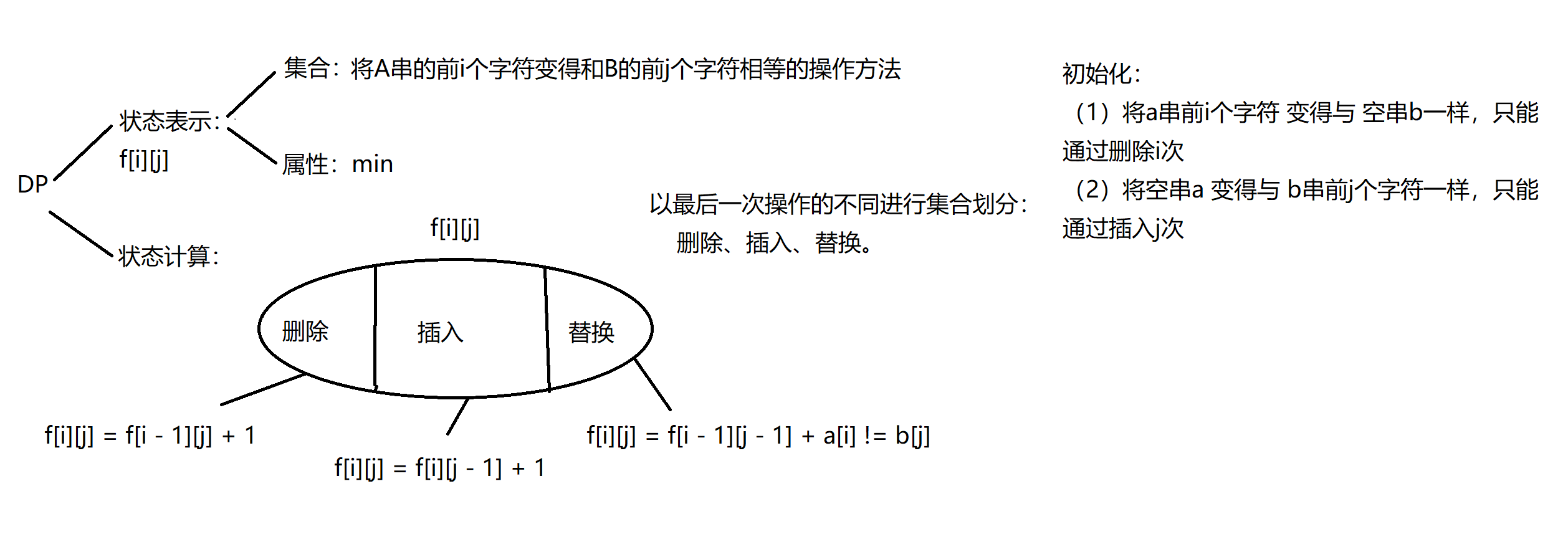
​ 对一个字符串A进行和删除、插入、替换的操作，使得A字符串与给定的B字符串相等，求最少的操作次数。

思路：

​ 根据最后一步操作的不同进行分析：
​ （1）删掉ai后，a与b一模一样，则需要满足a的1 ~ i - 1个字母与b的1 ~ j个字母匹配才能满足，所以先去掉最后一步，去找a的1 ~ i - 1变成b的1 ~ j - 1个字母匹配所需要的步数的最小值f[i - 1][j] + 1
​ （2）增加一个字母，a与b一模一样，则需要满足增加之前，a的1 ~ i个字母与b的 1 ~ j - 1个字母匹配f[i][j - 1] + 1
​ （3）改掉ai后，a与b一模一样，则需要满足的是a的1 ~ i - 1个字母与b的 1 ~ j - 1个字母匹配才行，这里分为两种情况，
​ 一种是ai与bi一样，不需要改，步数不用增加f[i - 1][j - 1],
​ 一种是ai与bi不一样，需要改，步数需要增加f[i - 1][j - 1] + 1;

​ 需要初始化的两种边界情况：
​ （1）a的前0个字母去匹配b的前j个字母时，只能通过增加的方式，且增加的步数为b的前j个字母的长度
​ （2）a的前i个字母去匹配b的前0个字母时，只能通过删除的方式，且删除的步数为a的前i个字母的长度

​ 集合：f[i][j]，将第一个子串前i个字符与第二个字串前j个字符变成一样的操作方法
​ 属性：min

​ 集合划分：删除、插入、替换三种不同操作
​ 状态计算：
​ （1）删除：需要a[1i - 1] = b[1j]
​ （2）插入：需要a[1i] = b[1j-1]
​ （3）替换：需要a[1i-1] = b[1j-1]

代码模板：

scanf("%d%s", &n, a + 1);
    scanf("%d%s", &m, b + 1);

    for (int i = 0; i <= m; i ++) f[0][i] = i;
    for (int i = 0; i <= n; i ++) f[i][0] = i;

    for (int i = 1; i <= n; i ++)
    {
        for (int j = 1; j <= m; j ++)
        {
            f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);    //删和增
            if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);  //改
            else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
        }
    }

注意：

​ 由于做dp需要涉及 i - 1 和 j - 1，故字符串的下标需要从1开始

3、最长上升子序列模型

描述：

​ 给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。

思路：

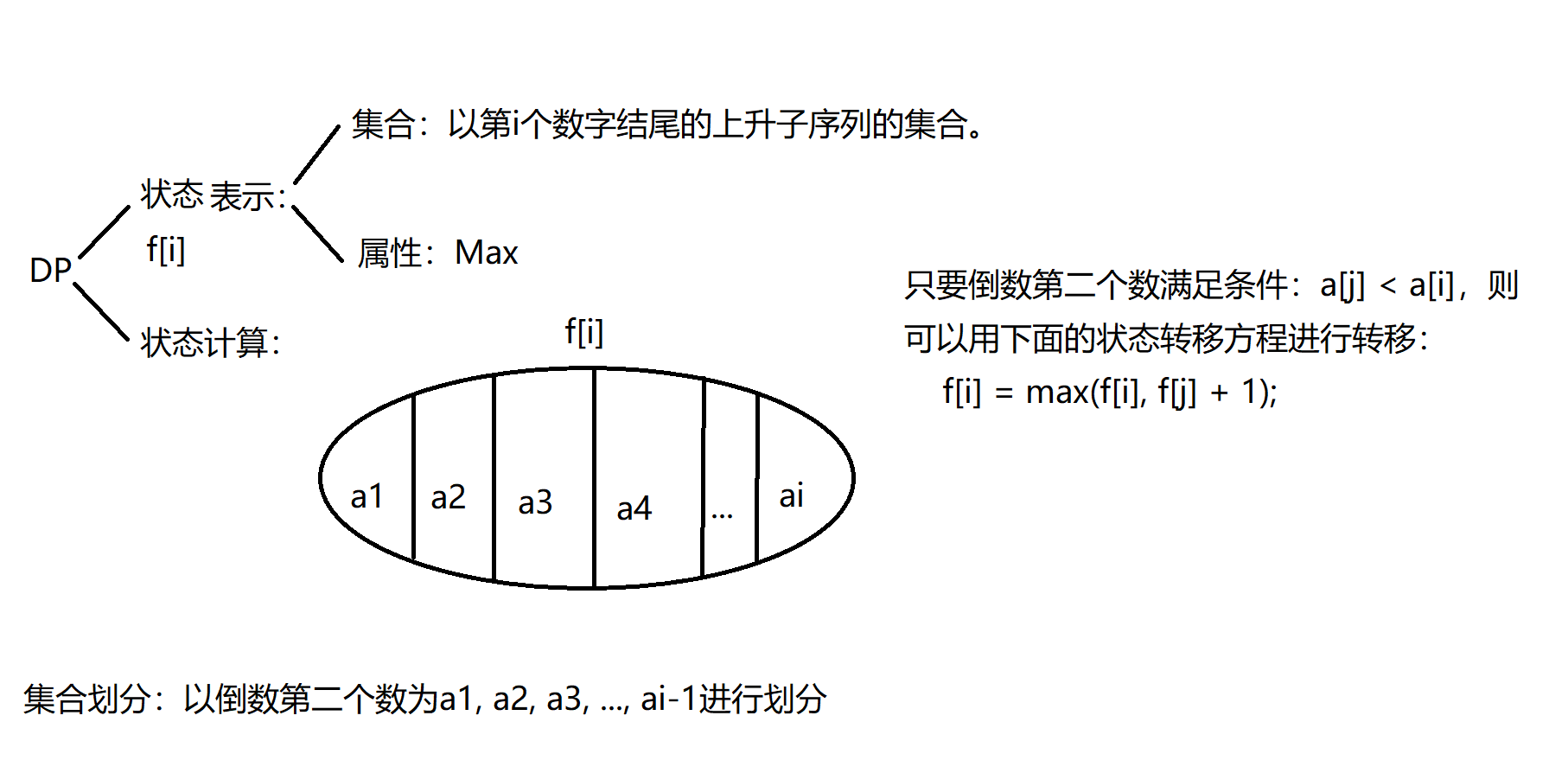
集合：f[i]表示所有以数字i结尾的上升子序列的集合
属性：max

状态划分：以倒数第二个数为1，2，3，4，，，，i - 1进行划分
只要倒数第二个数满足条件：a[j] < a[i]，则可以用下面的状态方程进行转移
f[i] = max(f[i], f[j] + 1);

代码：

int res = 0;
    for (int i = 1; i <= n; i ++)
    {
        f[i] = 1;
        for (int j = 1; j < n; j ++)
            if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
        res = max(f[i], res);
    }

注意：

​ （1）if (a[j] < a[i]) //用前面已经算好的最长上升序列更新第i个值的最长上升子序列，所以需要满足a[j]<a[i]，只要满足该条件，就说明目前的最长上升子序列为a[j]+1或者f[i]，f[i]指之前算出过的该点的最长上升子序列。

​ （2）关于为什么要初始化f[i] = 1？

​ 有一个边界，若前面没有比i小的，f[i]为1（自己为结尾）

​

4、最长公共子序列

描述：

​ 给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B的子序列的字符串长度最长是多少。

思路：

集合f[i][j]:表示所有在第一个序列前i个字母中出现，且在第二个序列前j个字母中出现的子序列
集合划分：以a[i],b[j]是否出现在子序列中划分
（1）00：都没有出现，f[i - 1][j - 1]
（2）01：a[i]没有出现，b[j]出现，由于直接求不好求，这里用f[i - 1][j]进行替代
（3）10：a[i]出现，b[j]没有出现，由于直接求不好求，这里用f[i][j - 1]进行替代
（4）11：a[i]、b[j]都出现，f[i - 1][j - 1] + 1

代码模板：

for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++)
        {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }

注意：

​ （2）、（3）步中的替代是不影响最终结果的：（2）中因为f[i - 1][j]表示所有在第一个序列中前i - 1个字母中出现，且在第二个序列前j个字母中出现的子序列，这里包含了a[i]不出现，b[j]出现的情况，虽然有部分重复，但由于我们求的是最大值，即使重复求，也不会影响我们所求的最大值，（3）同理。